궤도
[백준] 10816번 : 숫자 카드 2 본문
문제
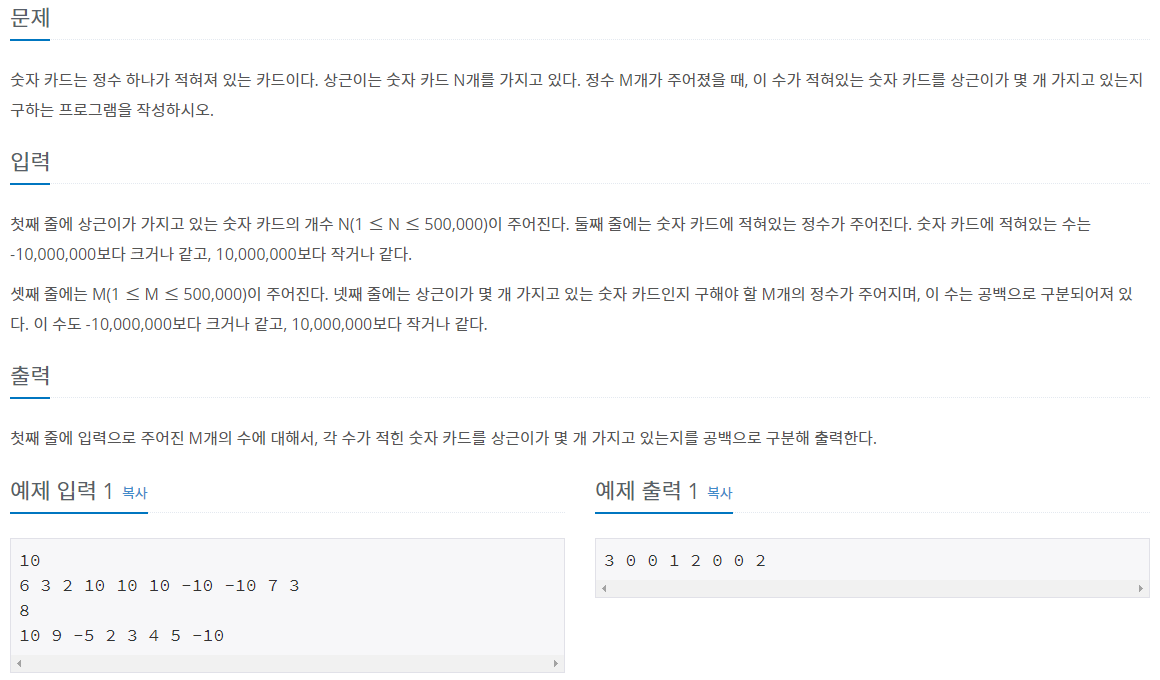
풀이
처음엔 value(값)와 num(등장 횟수)를 저장하는 구조체를 만들어서 중복없는 배열을 만든 뒤 이분 탐색했다.
그랬더니 시간초과가 발생했다. 그러다 예전에 C++ STL에 이분 탐색 같은게 있었던 것 같은 그런 기분이 들어 검색했더니
세상에 있었다.
www.cplusplus.com/reference/algorithm/lower_bound/?kw=lower_bound
lower_bound - C++ Reference
function template std::lower_bound default (1)template ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last, const T& val); custom (2)template ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last, const T
www.cplusplus.com
www.cplusplus.com/reference/algorithm/upper_bound/?kw=upper_bound
upper_bound - C++ Reference
function template std::upper_bound default (1)template ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last, const T& val); custom (2)template ForwardIterator upper_bound (ForwardIterator first, ForwardIterator last, const T
www.cplusplus.com
lower_bound 함수는 특정 배열과 찾고자 하는 key값이 있을 때 그 key값이 존재한다면 처음으로 등장하는 index를 반환한다. 만약 존재하지 않는 값이라면 배열 맨 끝의 index를 반환한다.
upper_bound 함수는 특정 배열과 찾고자 하는 key값이 있을 때 그 key값이 존재한다면 마지막으로 등장하는 index의 다음 값을 반환한다. 만약 존재하지 않는 값이라면 배열 맨 끝의 index를 반환한다.
그래서 이 함수를 써서 쉽게 풀렸지만...영 찝찝한 기분이 들어 저 함수를 직접 구현하기로 했다...
소스코드
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
//lower_bound, upper_bound 함수는 이진탐색으로 특정 수가 처음 등장하는 지점과 마지막으로 등장하는 지점을 찾아냄
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int N, M, input, target;
vector<int> cards;
cin >> N;
for (int i = 0; i < N; i++) {
cin >> input;
cards.push_back(input);
}
sort(cards.begin(), cards.end());
cin >> M;
for (int i = 0; i < M; i++) {
cin >> target;
cout << (upper_bound(cards.begin(), cards.end(), target) - cards.begin()) -
(lower_bound(cards.begin(), cards.end(), target) - cards.begin()) << ' ';
}
}이건 함수를 사용한 소스코드다.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<int> cards;
int lowerSearch(int target, int left, int right) { //해당 수가 처음으로 등장하는 위치
while (left <= right) {
int mid = (left + right) / 2;
if (target <= cards[mid]) //왼쪽 탐색
right = mid - 1;
else if (target > cards[mid]) //오른쪽 탐색
left = mid + 1;
}
return right + 1;
}
int upperSearch(int target, int left, int right) { //해당 수가 마지막으로 등장하는 위치
while (left <= right) {
int mid = (left + right) / 2;
if (target < cards[mid]) //왼쪽 탐색
right = mid - 1;
else if (target >= cards[mid]) //오른쪽 탐색
left = mid + 1;
}
return right + 1;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
int N, M, input, target;
cin >> N;
for (int i = 0; i < N; i++) {
cin >> input;
cards.push_back(input);
}
sort(cards.begin(), cards.end()); //정렬
cin >> M;
for (int i = 0; i < M; i++) {
cin >> target;
cout << upperSearch(target, 0, cards.size() - 1) - lowerSearch(target, 0, cards.size() - 1) << ' ';
}
}이건 직접 구현한 버전이다.
간단한 비교를 위해 이분 탐색 코드를 가져오겠다.
bool binarySearch(int target, int left, int right) {
while (left <= right) {
int mid = (left + right) / 2;
if (target == A[mid])
return true;
else if (target < A[mid]) //왼쪽 탐색
right = mid - 1;
else if (target > A[mid]) //오른쪽 탐색
left = mid + 1;
}
return false;
}
int lowerSearch(int target, int left, int right) { //해당 수가 처음으로 등장하는 위치
while (left <= right) {
int mid = (left + right) / 2;
if (target <= cards[mid]) //왼쪽 탐색
right = mid - 1;
else if (target > cards[mid]) //오른쪽 탐색
left = mid + 1;
}
return right + 1;
}
int upperSearch(int target, int left, int right) { //해당 수가 마지막으로 등장하는 위치
while (left <= right) {
int mid = (left + right) / 2;
if (target < cards[mid]) //왼쪽 탐색
right = mid - 1;
else if (target >= cards[mid]) //오른쪽 탐색
left = mid + 1;
}
return right + 1;
}lowerSearch와 upperSearch는 target을 찾아도 계속 이동해야 한다.
그렇기 때문에 target==A[mid] 부분이 빠지고 아래 두 조건 중 하나에 흡수돼야 했는데,
lowerSearch에 경우 왼쪽 탐색에, upperSearch에 경우 오른쪽 탐색에 흡수됐다.
그 이유를 자세하게 설명하면 이해도 어렵고 사실 내가 설명하기도 어려워서 그냥 간단하게 말하자면
lowerSearch는 계속 왼쪽으로 가야하니까 왼쪽 탐색에 흡수한거고
upperSearch는 계속 오른쪽으로 가야하니까 오른쪽 탐색에 흡수한 것이다.




