목록이분 탐색 (8)
궤도
 [백준] 14003번 : 가장 긴 증가하는 부분 수열 5
[백준] 14003번 : 가장 긴 증가하는 부분 수열 5
문제 풀이 난이도는 플레티넘이지만 이전에 푼 2문제를 합치면 쉽게 풀 수 있어서 풀었다. myunji.tistory.com/324?category=1154147 [백준] 14002번 : 가장 긴 증가하는 부분 수열 4 문제 풀이 myunji.tistory.com/214 [백준] 11053번 : 가장 긴 증가하는 부분 수열 문제 풀이 대표적인 동적계획법 문제이다. 증가하는 부분 수열을 담은 max_num이란 배열이 있다고 하자. max_num의 상태는 다 myunji.tistory.com 이 문제에서 수열을 출력해보았고 myunji.tistory.com/270 [백준] 12015번 : 가장 긴 증가하는 부분 수열 2 문제 풀이 myunji.tistory.com/214 [백준] 11053번 : 가장 긴 증가..
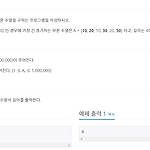 [백준] 12015번 : 가장 긴 증가하는 부분 수열 2
[백준] 12015번 : 가장 긴 증가하는 부분 수열 2
문제 풀이 myunji.tistory.com/214 [백준] 11053번 : 가장 긴 증가하는 부분 수열 문제 풀이 대표적인 동적계획법 문제이다. 증가하는 부분 수열을 담은 max_num이란 배열이 있다고 하자. max_num의 상태는 다음과 같다. 10 20 30 현재 max_num의 길이는 3이니 가장 긴 증가하는 부분 수 myunji.tistory.com 이 문제랑 똑같이 접근할 것이다. 위 문제에서는 LIS 수열을 만들고, 새로운 입력에 대해 LIS 수열의 마지막 원소부터 0번째 원소까지 이동하며 하나하나 비교하며 원소가 들어갈 위치를 찾아줬다. 이 부분에 대한 시간 복잡도는 O(n)이다. 만약 새로운 입력의 위치를 찾아주는 과정을 이분 탐색으로 하면 시간 복잡도가 O(logn)이 될 것이다. 새..
 [백준] 1300번 : K번째 수
[백준] 1300번 : K번째 수
문제 풀이 별별 뻘짓을 많이 했다... 일단 당연히 nxn의 배열을 실제로 저장한다거나, 배열 B를 만든다거나 하면 안된다. /* 생각(aka. 뻘짓) 일단 4x4의 행렬을 그려봤다. 그러다가 놀라운 사실을 하나 발견했다. i+j=2k(짝수라는 뜻)인 모든 A[i][j]에 대해 A[k][k]가 가장 크다는 것이었다. 그니까...4x4 행렬이 있다고 하자. A[2][2] = 4이다. i+j=4인 다른 A[i][j]를 보면, A[1][3] = 3, A[3][1] =3이 있다. 그래서 이걸 보고 left를 (1, 1), right를 (n, n)으로 한 뒤 그 둘의 mid를 구해서 계산하고 어쩌구...하는 식으로 했는데...망했다. */ 결국 검색을 했고 내 접근이 반은 맞고 반은 틀렸다는 것을 알았다. 반까지..
 [백준] 2110번 : 공유기 설치
[백준] 2110번 : 공유기 설치
문제 풀이 myunji.tistory.com/264?category=1154147 [백준] 1654번 : 랜선 자르기 문제 풀이 parametric search 문제라고 써있었다. 근데 난 이게 뭔지 모르니 검색을 해보았다. www.crocus.co.kr/1000 파라매트릭 서치(Parametric Search) 목차 1. 파라매트릭 서치(Parametric Search)란? 2. 예.. myunji.tistory.com 이 문제와 풀이가 같다. 굳이 다른 점을 찾자면 저 문제는 특정 길이에 대해 자를 수 있는 랜선의 수를 리턴한다면 이건 특정 거리에 대해 설치 가능 여부를 리턴 받는다는 점..? 이렇게 말하면 뭐가 다른 건지 감이 안올테니 바로 코드로 넘어가겠다. 소스코드 #include #includ..
 [백준] 2805번 : 나무 자르기
[백준] 2805번 : 나무 자르기
문제 풀이 myunji.tistory.com/264?category=1154147 [백준] 1654번 : 랜선 자르기 문제 풀이 parametric search 문제라고 써있었다. 근데 난 이게 뭔지 모르니 검색을 해보았다. www.crocus.co.kr/1000 파라매트릭 서치(Parametric Search) 목차 1. 파라매트릭 서치(Parametric Search)란? 2. 예.. myunji.tistory.com 이 문제랑 풀이가 동일하다. 그러니 딱히 설명하지 않도록 하겠다. 소스코드 #include #include #include using namespace std; typedef long long ll; int N, M; vector tree; ll cntTree(ll length) { /..
 [백준] 1654번 : 랜선 자르기
[백준] 1654번 : 랜선 자르기
문제 풀이 parametric search 문제라고 써있었다. 근데 난 이게 뭔지 모르니 검색을 해보았다. www.crocus.co.kr/1000 파라매트릭 서치(Parametric Search) 목차 1. 파라매트릭 서치(Parametric Search)란? 2. 예시를 통한 파라매트릭 서치(Parametric Search) 3. 시간 복잡도 4. 정리 5. 관련 문제 1. 파라매트릭 서치(Parametric Search)란? Parametric Search에 대해.. www.crocus.co.kr 이 글을 보고 완벽하게 이해했다. 그렇다면 이 문제에서 left와 right는 무엇일까? 랜선의 길이가 0cm일 수는 없으니까 left는 1일 것이다. 그리고 막연하게 right는 가장 짧은 랜선의 길이와 ..
 [백준] 10816번 : 숫자 카드 2
[백준] 10816번 : 숫자 카드 2
문제 풀이 처음엔 value(값)와 num(등장 횟수)를 저장하는 구조체를 만들어서 중복없는 배열을 만든 뒤 이분 탐색했다. 그랬더니 시간초과가 발생했다. 그러다 예전에 C++ STL에 이분 탐색 같은게 있었던 것 같은 그런 기분이 들어 검색했더니 세상에 있었다. www.cplusplus.com/reference/algorithm/lower_bound/?kw=lower_bound lower_bound - C++ Reference function template std::lower_bound default (1)template ForwardIterator lower_bound (ForwardIterator first, ForwardIterator last, const T& val); custom (2)te..
 [백준] 1920번 : 수 찾기
[백준] 1920번 : 수 찾기
문제 풀이 이분 탐색은 문제의 크기를 반으로 잘라가며 답을 찾는 알고리즘이다. 이런 문제일 때는 주어진 배열을 정렬하고, 배열의 가운데 값(mid)과 목표로 하는 값(target)을 비교한다. 만약 mid==target이면 답을 찾은 것이니 바로 리턴하고 midtarget이면 mid를 기준으로 배열을 잘라 그 왼쪽만 탐색하면 된다. 소스코드 #include #include using namespace std; int A[1000000]; bool binarySearch(int target, int left, int right) { while (left A[mid]) //오른쪽 탐색 left = mid + 1; } return false; } int main() { ios::sync_with_stdio(f..
