[백준] 14500번 : 테트로미노

문제

 

---

풀이

 

가능한 모양을 하나하나 분리해서 찾는건 이 문제가 브루트포스라고 해도 너무한 방법이다.

 

보라색 조각을 제외한 나머지 4개의 조각은 백트래킹으로 탐색할 수 있는 조각이다.

백트래킹으로 탐색할 수 있다는걸 쉽게 설명하면

 

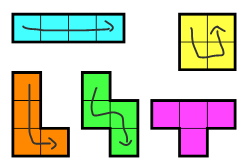
한붓 그리기처럼 탐색할 수 있단 뜻이다.

 

그럼 보라색 조각을 제외한 나머지 조각은 백트래킹으로 처리한다고 치고, 보라색 조각은 어떻게 처리할까?

 

이런 조각 하나가 있다고 하자. 이 조각을 기준으로 상하좌우에 조각을 붙이면

 

이런 + 모양이 될 것이다.

여기에 상하좌우 중 하나의 조각만 빼면 가능한 모든 보라색 조각의 경우가 나올 것이다.

---

소스코드

 

링크 <- 최근 리팩토링한 코드

#include <iostream>
#include <utility>

using namespace std;

int matrix[500][500];
int local_max, N, M;
pair<int, int> dir[4] = {{-1, 0},  //상
                         {1,  0},  //하
                         {0,  -1}, //좌
                         {0,  1}}; //우

void horn(int row, int col, int sum) { //matrix[row][col]가 + 모양의 정 가운데가 될 것
    int cnt = 0;
    int arr[4] = {0}; //상하좌우의 값 저장

    for (int i = 0; i < 4; i++) {
        int nr = row + dir[i].first;
        int nc = col + dir[i].second;

        if ((nr >= 0) && (nr < N) && (nc >= 0) && (nc < M)) { //범위에 들어오면 저장
            cnt++;
            arr[i] = matrix[nr][nc];
            sum += matrix[nr][nc];
        }
    }

    if ((cnt == 3) && (sum > local_max)) //보라색 조각과 같은 모양
        local_max = sum;
    else if (cnt == 4) { // + 모양
        for (int i = 0; i < 4; i++) { //상하좌우의 값 중 하나씩 빼보며 최댓값 확인
            int tmp = sum;

            tmp -= arr[i];
            if (tmp > local_max)
                local_max = tmp;
        }
    }
    return;
}

void tetromino(int row, int col, int num, int sum) {
    if (num == 4) { //백트래킹 종료 조건
        if (sum > local_max)
            local_max = sum;
        return;
    }

    int value = matrix[row][col];
    for (int i = 0; i < 4; i++) {
        int nr = row + dir[i].first;
        int nc = col + dir[i].second;

        if ((nr >= 0) && (nr < N) && (nc >= 0) && (nc < M) && (matrix[nr][nc] != 0)) { //범위에 들어왔고 unvisited 라면
            matrix[row][col] = 0; //visited 처리
            tetromino(nr, nc, num + 1, sum + matrix[nr][nc]); //백트래킹 탐색
            matrix[row][col] = value; //unvisited 처리
        }
    }
}

int main() {
    int result = 0;

    cin >> N >> M;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++)
            cin >> matrix[i][j];
    }

    local_max = 0; //matrix[i][j]를 포함해서 만들 수 있는 모든 블럭의 최댓값
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            horn(i, j, matrix[i][j]); //보라색 블럭 처리
            tetromino(i, j, 1, matrix[i][j]); //나머지 모양 처리

            if (local_max > result) //최댓값?
                result = local_max;
        }
    }
    cout << result;
}

전체 소스코드다.

 

int matrix[500][500];
int local_max, N, M;
pair<int, int> dir[4] = {{-1, 0},  //상
                         {1,  0},  //하
                         {0,  -1}, //좌
                         {0,  1}}; //우

상하좌우 탐색을 해야하니 dir 페어 배열을 만들었다.

칸들의 정보는 matrix에 저장할거고... local_max의 쓰임은 이따가 설명하도록 하겠다.

 

    local_max = 0; //matrix[i][j]를 포함해서 만들 수 있는 모든 블럭의 최댓값
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < M; j++) {
            horn(i, j, matrix[i][j]); //보라색 블럭 처리
            tetromino(i, j, 1, matrix[i][j]); //나머지 모양 처리

            if (local_max > result) //최댓값?
                result = local_max;
        }
    }

matrix[i][j]에 대해 이 조각을 포함한 모든 가능한 블럭을 찾을 것이다. 그리고 그 중의 최댓값을 local_max에 저장할 것이다.

물론 이러면 중복되는 블럭이 생기긴 하겠지만 그정돈 괜찮다.

중복되는 블럭을 제외하는 방법을 알고 있긴 하지만 귀찮다.

 

먼저 horn 함수를 호출하여 보라색 블럭을 처리한 뒤, tetromino 함수에서 나머지 블럭을 처리한다.

 

void horn(int row, int col, int sum) { //matrix[row][col]가 + 모양의 정 가운데가 될 것
    int cnt = 0;
    int arr[4] = {0}; //상하좌우의 값 저장

    for (int i = 0; i < 4; i++) {
        int nr = row + dir[i].first;
        int nc = col + dir[i].second;

        if ((nr >= 0) && (nr < N) && (nc >= 0) && (nc < M)) { //범위에 들어오면 저장
            cnt++;
            arr[i] = matrix[nr][nc];
            sum += matrix[nr][nc];
        }
    }

    if ((cnt == 3) && (sum > local_max)) //보라색 조각과 같은 모양
        local_max = sum;
    else if (cnt == 4) { // + 모양
        for (int i = 0; i < 4; i++) { //상하좌우의 값 중 하나씩 빼보며 최댓값 확인
            int tmp = sum;

            tmp -= arr[i];
            if (tmp > local_max)
                local_max = tmp;
        }
    }
    return;
}

보라색 조각을 처리하는 horn 함수이다.

상하좌우가 범위 내에 있는 탐색 가능 좌표라면 cnt도 늘려주고 sum에도 합해주고 추가로 arr 배열에 정보도 저장해둔다.

 

cnt가 3은 되어야 보라색 조각을 만들 수 있다. cnt가 3이라면 굳이 조각을 하나 뺄 필요가 없다.

cnt가 4라면 상하좌우의 값 중 하나씩 빼본다.

 

void tetromino(int row, int col, int num, int sum) {
    if (num == 4) { //백트래킹 종료 조건
        if (sum > local_max)
            local_max = sum;
        return;
    }

    int value = matrix[row][col];
    for (int i = 0; i < 4; i++) {
        int nr = row + dir[i].first;
        int nc = col + dir[i].second;

        if ((nr >= 0) && (nr < N) && (nc >= 0) && (nc < M) && (matrix[nr][nc] != 0)) { //범위에 들어왔고 unvisited 라면
            matrix[row][col] = 0; //visited 처리
            tetromino(nr, nc, num + 1, sum + matrix[nr][nc]); //백트래킹 탐색
            matrix[row][col] = value; //unvisited 처리
        }
    }
}

나머지 블럭을 처리하는 tetromino 함수이다.

그냥 전형적인 백트래킹 함수의 형태다.