[백준] 10971번 : 외판원 순회 2

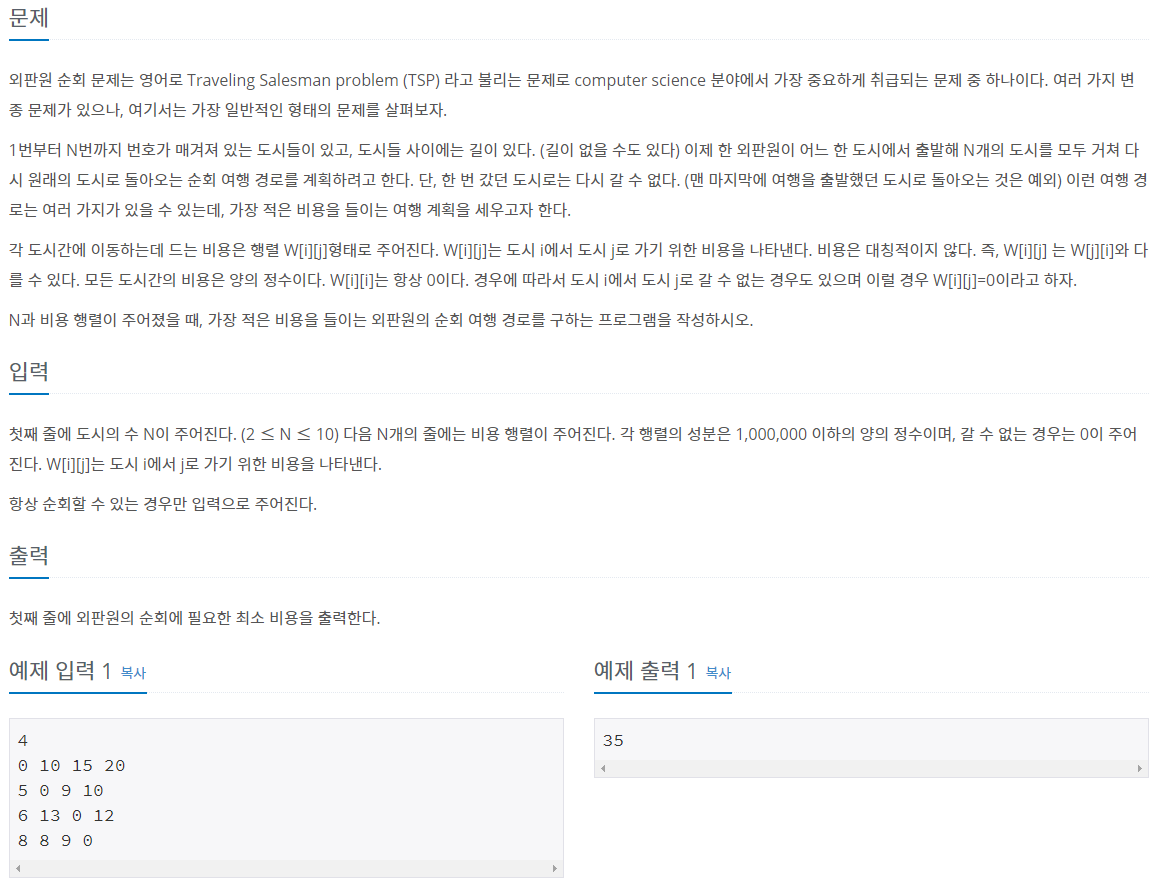
문제

 

---

풀이

 

 

보통의 최단거리 문제와 달리 TSP 문제는 처음 출발지점으로 돌아와야 한다.

 

그냥 백트래킹으로 경로를 끝까지 찾다가 마지막 지점에서 처음 출발지점으로 돌아올 수 있는 길이 있는지만 확인하면 된다.

---

소스코드

 

#include <iostream>

using namespace std;

int matrix[10][10], N, cost, min_cost = -1;
bool visited[10];

//실시간으로 값을 갱신하는 코드는 갱신을 취소하는 부분을 반드시 넣어야 함
void backtracking(int start, int cur, int num) {
    if (num == N) { //종료 조건
        if (matrix[cur][start] != 0) { //처음 시작점으로 돌아올 수 있는가?
            cost += matrix[cur][start];
            if ((min_cost == -1) || (cost < min_cost)) //최소 비용 갱신
                min_cost = cost;
            cost -= matrix[cur][start];
        }
        return;
    }
    for (int i = 0; i < N; i++) {
        if ((matrix[cur][i] != 0) && !visited[i]) { //길이 있고 방문한 적 없는 도시라면
            visited[i] = true; //visited 처리
            cost += matrix[cur][i];
            if ((min_cost == -1) || (cost < min_cost)) //지금까지의 cost가 min_cost보다 작을 때만 min_cost일 가능성이 있음(=탐색할 가치가 있음)
                backtracking(start, i, num + 1);
            visited[i] = false; //unvisited 처리
            cost -= matrix[cur][i];
        }
    }
}

int main() {
    cin >> N;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++)
            cin >> matrix[i][j];
    }
    for (int i = 0; i < N; i++) { //도시 i를 출발점으로 했을 때의 최소 비용
        cost = 0;
        visited[i] = true; //visited 처리
        backtracking(i, i, 1);
        visited[i] = false; //unvisited 처리
    }
    cout << min_cost;
}

경로의 비용을 계산하는 cost 변수를 잘 관리해야 한다.

 

    for (int i = 0; i < N; i++) { //도시 i를 출발점으로 했을 때의 최소 비용
        cost = 0;
        visited[i] = true; //visited 처리
        backtracking(i, i, 1);
        visited[i] = false; //unvisited 처리
    }

main에선 도시 i를 처음 출발 지점으로 하고 n번 백트래킹 함수를 호출한다.

 

//실시간으로 값을 갱신하는 코드는 갱신을 취소하는 부분을 반드시 넣어야 함
void backtracking(int start, int cur, int num) {
    if (num == N) { //종료 조건
        if (matrix[cur][start] != 0) { //처음 시작점으로 돌아올 수 있는가?
            cost += matrix[cur][start];
            if ((min_cost == -1) || (cost < min_cost)) //최소 비용 갱신
                min_cost = cost;
            cost -= matrix[cur][start];
        }
        return;
    }
    for (int i = 0; i < N; i++) {
        if ((matrix[cur][i] != 0) && !visited[i]) { //길이 있고 방문한 적 없는 도시라면
            visited[i] = true; //visited 처리
            cost += matrix[cur][i];
            if ((min_cost == -1) || (cost < min_cost)) //지금까지의 cost가 min_cost보다 작을 때만 min_cost일 가능성이 있음(=탐색할 가치가 있음)
                backtracking(start, i, num + 1);
            visited[i] = false; //unvisited 처리
            cost -= matrix[cur][i];
        }
    }
}

백트래킹 함수다.

 

    for (int i = 0; i < N; i++) {
        if ((matrix[cur][i] != 0) && !visited[i]) { //길이 있고 방문한 적 없는 도시라면
            visited[i] = true; //visited 처리
            cost += matrix[cur][i];
            if ((min_cost == -1) || (cost < min_cost)) //지금까지의 cost가 min_cost보다 작을 때만 min_cost일 가능성이 있음(=탐색할 가치가 있음)
                backtracking(start, i, num + 1);
            visited[i] = false; //unvisited 처리
            cost -= matrix[cur][i];
        }
    }

길도 이어져있고, 방문한 적도 없다면 방문 처리를 해주고 cost 변수를 갱신해준다.

근데 만약 이 cost가 이미 min_cost보다 크거나 같다면 굳이 더이상 탐색할 필요가 없으므로 그렇지 않을때만 탐색한다.

 

그리고 나서 unvisited 처리를 할 때 cost 변수도 같이 처리해야 한다. 이 부분을 놓쳐서 좀 헤맸다.

 

    if (num == N) { //종료 조건
        if (matrix[cur][start] != 0) { //처음 시작점으로 돌아올 수 있는가?
            cost += matrix[cur][start];
            if ((min_cost == -1) || (cost < min_cost)) //최소 비용 갱신
                min_cost = cost;
            cost -= matrix[cur][start];
        }
        return;
    }

종료조건은 탐색한 도시의 수가 N과 같을 때이다.

이때 마지막 지점에서 출발지점으로 갈 수 있는 길이 있는지 확인하고 cost 변수를 갱신한다.

min_cost의 갱신 여부를 확인한 후, 아까와 같이 cost 변수의 값을 다시 처리한다.