[백준] 9370번 : 미확인 도착지

문제

 

---

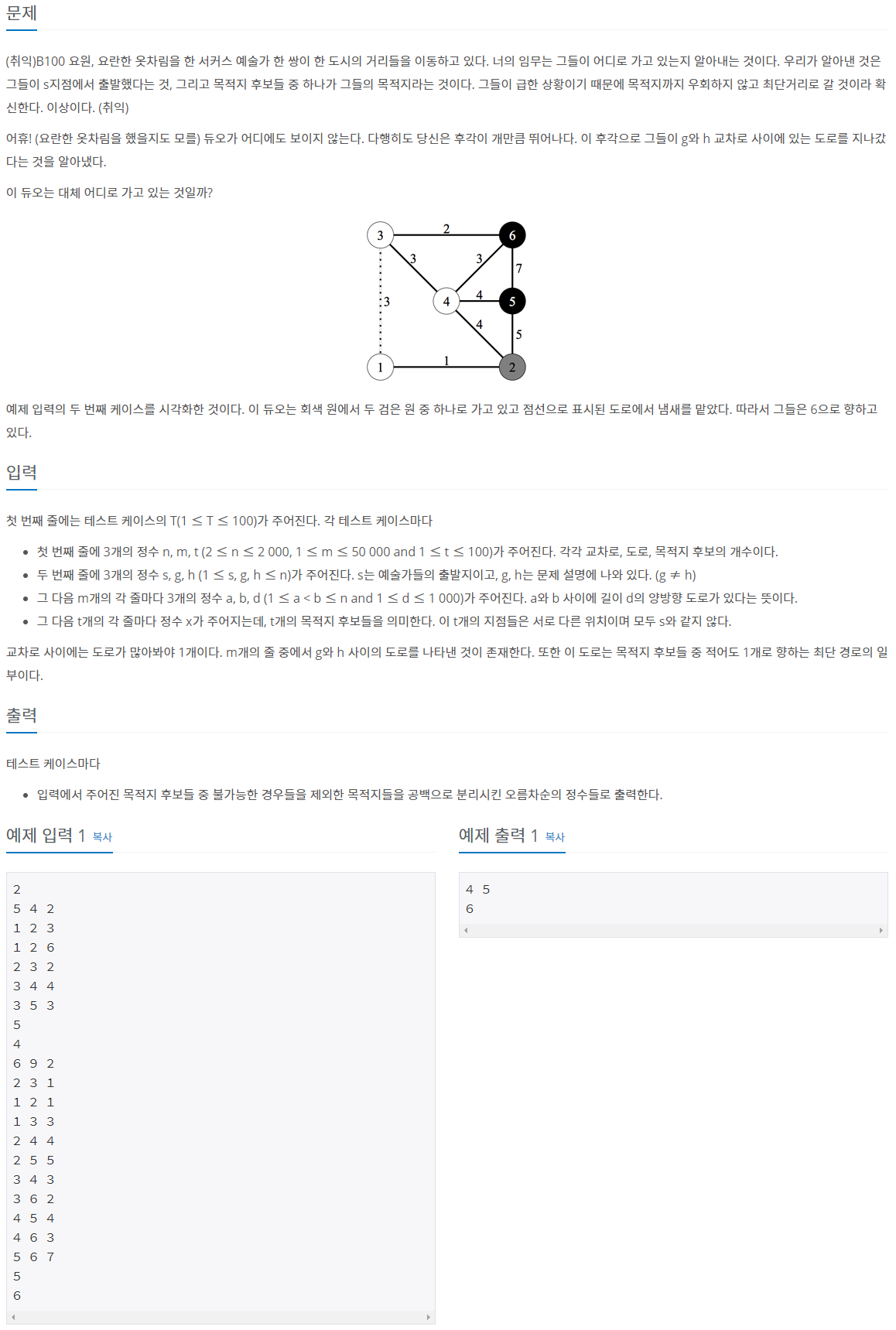
풀이

 

굳이 안그래도 될걸 억지로 어렵게 만들었다는 느낌이 드는 문제다.

 

myunji.tistory.com/345

[백준] 1504번 : 특정한 최단 경로

논리는 이 문제랑 같다.

 

일단 s->t 최단 거리를 구한다. 만약 s->g->h->t 또는 s->h->g->t 의 최단거리와 s->t와 같다면 목적지가 될 수 있다.

---

소스코드

 

#include <iostream>
#include <vector>
#include <queue>
#include <utility>
#include <string>
#include <algorithm>

using namespace std;

const int INF = 1e9 * 2;
typedef pair<int, int> pp;

vector<vector<pp>> graph; //graph[i][j].first = dest, graph[i][j].second = weight
vector<int> V_dist; //INF로 초기화
vector<bool> visited; //방문 체크
priority_queue<pp, vector<pp>, greater<pp>> min_dist; //min-heap, min_dist.first = distance, min_dist.second = source
vector<int> result;

void init(int size) { //초기화
    V_dist.assign(size, INF);
    visited.assign(size, false);
}

void dijkstra(int start) {
    int new_dist;

    V_dist[start] = 0; //시작점의 거리는 0
    min_dist.push(make_pair(V_dist[start], start)); //거리와 source 투입

    while (!min_dist.empty()) { //우선순위 큐가 비어있지 않을 때
        int dist = min_dist.top().first; //현재 노드 까지의 최단 거리
        int source = min_dist.top().second; //노드
        min_dist.pop();

        if (!visited[source]) { //방문한 적 없는 노드라면
            for (int i = 0; i < graph[source].size(); i++) { //해당 노드가 source인 모든 정점(dest)
                new_dist = dist + graph[source][i].second; //현재 노드까지의 최단거리 + source에서 dest까지의 weight
                if (new_dist < V_dist[graph[source][i].first]) { //이 값이 기존의 V_dist[dest]보다 작다면
                    V_dist[graph[source][i].first] = new_dist; //dest의 최단거리 갱신
                    min_dist.push(make_pair(new_dist, graph[source][i].first)); //우선순위 큐에 거리와 dest 노드 정보 삽입
                }
            }
        }
        visited[source] = true; //source 노드 방문 처리
    }
}

void localDijkstra(int start, int size, int weight, vector<int> candi, vector<int> dist) { //g, h에서 다익스트라 후 경유 확인
    init(size);
    dijkstra(start);
    for (int j = 0; j < candi.size(); j++) {
        if ((weight + V_dist[candi[j]]) == dist[j])
            result.push_back(candi[j]);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int T, n, m, t, s, g, h, a, b, d, x, gh_length, to_g, to_h;

    cin >> T;
    for (int i = 0; i < T; i++) {
        vector<int> dest_candi, dest_dist;

        cin >> n >> m >> t >> s >> g >> h;
        graph.assign(n + 1, vector<pp>(0));
        for (int j = 0; j < m; j++) {
            cin >> a >> b >> d;
            if ((a == g && b == h) || (a == h && b == g)) //gh 사이의 거리
                gh_length = d;
            graph[a].push_back(make_pair(b, d));
            graph[b].push_back(make_pair(a, d));
        }
        for (int j = 0; j < t; j++) {
            cin >> x;
            dest_candi.push_back(x);
        }
        sort(dest_candi.begin(), dest_candi.end()); //도착지점 후보들 정렬

        init(n + 1);
        dijkstra(s); //s를 시작점으로 한 다익스트라
        for (int j = 0; j < t; j++) //각 도착지점 후보들까지의 최단거리 저장
            dest_dist.push_back(V_dist[dest_candi[j]]);
        to_g = V_dist[g]; //s->g 까지의 거리
        to_h = V_dist[h]; //s->h 까지의 거리

        localDijkstra(g, n + 1, to_h + gh_length, dest_candi, dest_dist); //s->h->g->t가 t까지의 최단거리와 동일한지 확인
        localDijkstra(h, n + 1, to_g + gh_length, dest_candi, dest_dist); //s->g->h->t가 t까지의 최단거리와 동일한지 확인

        sort(result.begin(), result.end()); //정렬
        result.erase(unique(result.begin(), result.end()), result.end()); //중복제거
        for (int j = 0; j < result.size(); j++) //출력
            cout << result[j] << ' ';
        cout << '\n';
        result.clear(); //초기화
    }
}

전체 소스코드다. 다익스트라 부분은 설명하지 않겠다.

 

        for (int j = 0; j < m; j++) {
            cin >> a >> b >> d;
            if ((a == g && b == h) || (a == h && b == g)) //gh 사이의 거리
                gh_length = d;
            graph[a].push_back(make_pair(b, d));
            graph[b].push_back(make_pair(a, d));
        }

그래프 벡터에 간선 정보를 넣으면서 g-h 간선이 있는지 확인한다. 찾으면 gh_length에 저장한다.

g와 h 사이의 거리라는 뜻이다.

 

        for (int j = 0; j < t; j++) {
            cin >> x;
            dest_candi.push_back(x);
        }
        sort(dest_candi.begin(), dest_candi.end()); //도착지점 후보들 정렬

도착지점 후보들을 입력받고 오름차순으로 정렬한다.

 

        init(n + 1);
        dijkstra(s); //s를 시작점으로 한 다익스트라
        for (int j = 0; j < t; j++) //각 도착지점 후보들까지의 최단거리 저장
            dest_dist.push_back(V_dist[dest_candi[j]]);
        to_g = V_dist[g]; //s->g 까지의 거리
        to_h = V_dist[h]; //s->h 까지의 거리

시작점에 대해 다익스트라 알고리즘을 실행한다.

그리고 각 도착지점 후보들까지의 최단 거리를 dest_dist 벡터에 저장하고, g, h까지의 거리도 저장한다.

 

void init(int size) { //초기화
    V_dist.assign(size, INF);
    visited.assign(size, false);
}

init 함수는 그냥 초기화 함수다.

 

        localDijkstra(g, n + 1, to_h + gh_length, dest_candi, dest_dist); //s->h->g->t가 t까지의 최단거리와 동일한지 확인
        localDijkstra(h, n + 1, to_g + gh_length, dest_candi, dest_dist); //s->g->h->t가 t까지의 최단거리와 동일한지 확인

그리고 g, h에 대한 localDijkstra 함수를 실행해 가능한 도착지점을 체크한다.

 

void localDijkstra(int start, int size, int weight, vector<int> candi, vector<int> dist) { //g, h에서 다익스트라 후 경유 확인
    init(size);
    dijkstra(start);
    for (int j = 0; j < candi.size(); j++) {
        if ((weight + V_dist[candi[j]]) == dist[j])
            result.push_back(candi[j]);
    }
}

start=g일 때를 예로 들자면

g를 시작점으로 하는 다익스트라를 실행하고 도착지점 후보 정점 t에 대해

s->h->g->t와 s->t의 거리가 같은지 확인한다.

 

s->h와 h->g는 각각 to_h와 gh_length로 둘을 weight 변수로 합해 함수에 전달했다.

그래서 g->t인 V_dist[t]+weight가 dist[t](s->t)와 같다면 result에 t를 넣어준다.

 

        sort(result.begin(), result.end()); //정렬
        result.erase(unique(result.begin(), result.end()), result.end()); //중복제거
        for (int j = 0; j < result.size(); j++) //출력
            cout << result[j] << ' ';
        cout << '\n';
        result.clear(); //초기화

result 벡터는 정렬 후 중복을 제거하고, 다음 테스트 케이스를 위해 초기화 한다.