[백준] 16947번 : 서울 지하철 2호선

문제

 

---

풀이

 

굉장히 비효율적인 방법으로 풀었는데 시간초과가 나지 않았다.

문제를 풀고나서 효율적으로 작성한 코드를 몇개 봤지만 도통 이해가 되지 않아서...강해져서 돌아와야겠다.

 

아무튼 내가 한 비효율적인 방법은 정점의 개수만큼 dfs를 실행한 것이다.

최대 입력이 3,000이라 시간초과가 발생할 것이라고 생각했는데 그렇지 않았다.

사실 다른 효율적인 방법을 나름 시도해봤지만 영 제대로 풀리지가 않았다.

 

myunji.tistory.com/350

[백준] 4803번 : 트리

이 문제에서 그래프 내 사이클을 찾았다.

한 번 방문했던 정점을 또다시 방문하게 되는 그 최초지점에 사이클이 있다고 리턴하는 것인데...

그림으로 그려보면 이러하다.

 

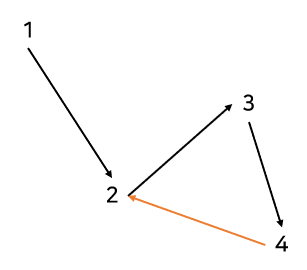
1부터 탐색을 한다고 하자.

 

1->2->3->4->2(사이클 최초 확인)

최초 시작점인 1과 사이클을 최초 확인한 2는 다른 정점이다.

 

4->2->1->3->4(사이클 최초 확인)

최초 시작점인 4와 사이클을 최초 확인한 4는 같은 정점이다.

 

그니까 사이클을 최초 확인한 그 시점에서 해당 정점이 시작점과 같다면 시작점은 사이클에 포함된 것이고, 아니라면 사이클에 포함되지 않은 것이다. 그래서 난 이걸 모든 정점에 대해 확인했다...

 

그리고 나서 사이클에 포함되지 않은 모든 정점에 대해 각각 bfs를 실행했는데 이렇게까지 했는데도 시간초과가 발생하지 않아서 참 신기할 따름이다.

---

소스코드

 

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

vector<vector<int>> graph;
vector<int> status;
vector<bool> cycle;
int isCycle;

void dfs(int start, int cur, int source) { //시작 정점, 현재 정점, 직전 정점
    if (status[cur]) { //이미 방문한 정점을 갔는데
        if (cur == start) //시작 정점이면 사이클
            isCycle = 1;
        else
            isCycle = 2; //사이클이 아님
        return;
    }
    status[cur] = 1; //방문 처리
    for (int i = 0; i < graph[cur].size() && !isCycle; i++) {
        if (graph[cur][i] != source) { //직전 정점이 아니면 연결된 정점 탐색
            dfs(start, graph[cur][i], cur);
        }
    }
}

int bfs(int start) {
    queue<int> q;

    status[start] = 1;
    q.push(start);
    while (!q.empty()) {
        int cur = q.front(); //현재 정점
        q.pop();
        if (cycle[cur]) //사이클인 정점을 만나면 리턴
            return status[cur] - 1;
        for (int i = 0; i < graph[cur].size(); i++) {
            if (!status[graph[cur][i]]) { //미방문 정점
                status[graph[cur][i]] = status[cur] + 1;
                q.push(graph[cur][i]);
            }
        }
    }
    return 0;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int N, first, second;

    cin >> N;
    graph.assign(N + 1, vector<int>(0));
    cycle.assign(N + 1, false);
    for (int i = 0; i < N; i++) {
        cin >> first >> second;
        graph[first].push_back(second);
        graph[second].push_back(first);
    }

    for (int i = 1; i <= N; i++) { //모든 정점에 대해 사이클에 포함된 정점이 맞는지 체크
        status.assign(N + 1, 0);
        isCycle = 0;
        dfs(i, i, -1);
        if (isCycle==1)
            cycle[i] = true;
    }

    for (int i = 1; i <= N; i++) { //모든 정점에 대해 사이클이면 0 출력, 아니면 bfs
        if (cycle[i])
            cout << 0 << ' ';
        else {
            status.assign(N + 1, 0);
            cout << bfs(i) << ' ';
        }
    }
}

전체 소스코드다.

 

    for (int i = 1; i <= N; i++) { //모든 정점에 대해 사이클에 포함된 정점이 맞는지 체크
        status.assign(N + 1, 0);
        isCycle = 0;
        dfs(i, i, -1);
        if (isCycle==1)
            cycle[i] = true;
    }

모든 정점에 대해 사이클에 포함된 정점인지 확인하고 cycle 벡터에 입력해준다.

 

void dfs(int start, int cur, int source) { //시작 정점, 현재 정점, 직전 정점
    if (status[cur]) { //이미 방문한 정점을 갔는데
        if (cur == start) //시작 정점이면 사이클
            isCycle = 1;
        else
            isCycle = 2; //사이클이 아님
        return;
    }
    status[cur] = 1; //방문 처리
    for (int i = 0; i < graph[cur].size() && !isCycle; i++) {
        if (graph[cur][i] != source) { //직전 정점이 아니면 연결된 정점 탐색
            dfs(start, graph[cur][i], cur);
        }
    }
}

4803번의 코드에서 최초로 발견한 사이클 정점이 시작 정점과 같은지 확인하는 부분만 추가했다.

 

    for (int i = 1; i <= N; i++) { //모든 정점에 대해 사이클이면 0 출력, 아니면 bfs
        if (cycle[i])
            cout << 0 << ' ';
        else {
            status.assign(N + 1, 0);
            cout << bfs(i) << ' ';
        }
    }

모든 정점에 대해 사이클에 포함된 정점이라면 0을 출력하고

아니라면 다시 해당 정점에 대한 bfs를 실행해 거리를 구한다.

 

int bfs(int start) {
    queue<int> q;

    status[start] = 1;
    q.push(start);
    while (!q.empty()) {
        int cur = q.front(); //현재 정점
        q.pop();
        if (cycle[cur]) //사이클인 정점을 만나면 리턴
            return status[cur] - 1;
        for (int i = 0; i < graph[cur].size(); i++) {
            if (!status[graph[cur][i]]) { //미방문 정점
                status[graph[cur][i]] = status[cur] + 1;
                q.push(graph[cur][i]);
            }
        }
    }
    return 0;
}

그냥 최단경로를 구할 때 사용하는 평범한 bfs다.