궤도
[백준] 17472번 : 다리 만들기 2 본문
문제
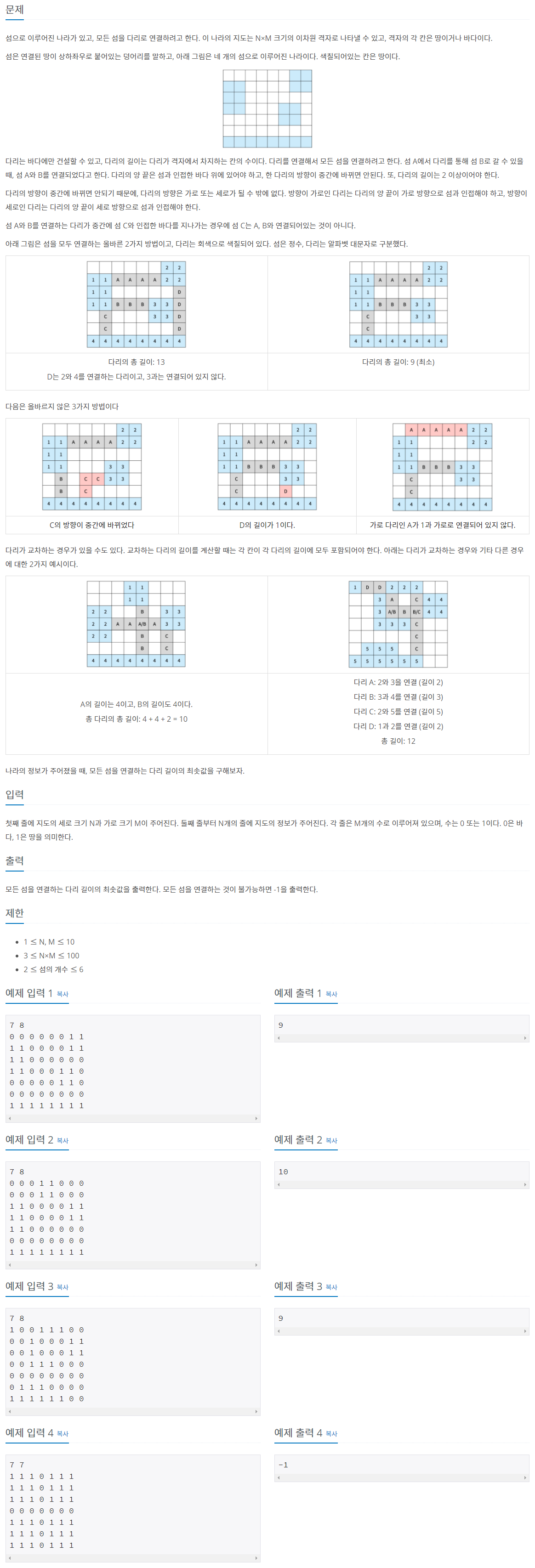
풀이
할 것이 굉장히 많다...
일단 최대 입력을 보니 브루트포스로 각 섬을 연결하는 모든 다리를 찾아도 될 것 같았다.
그렇다면 각 섬을 연결하는 다리를 어떻게 찾을 것이냐가 문제인데...
각각의 섬을 구분해야 하니 섬마다 다른 숫자로 라벨링하기로 했다.
[백준] 2146번 : 다리 만들기
문제 풀이 일단 다른 섬끼리 다리를 이어야 하기 때문에 각각의 섬을 구분해야 한다. 이런식으로 말이다. myunji.tistory.com/280 [백준] 2667번 : 단지번호붙이기 문제 풀이 문제 이름에 왜 띄어쓰기가
myunji.tistory.com
이 문제에서 섬을 구분했던 것과 같은 방법을 쓴다.
| 0 | 0 | 0 | 0 | 0 | 0 | 2 | 2 |
| 3 | 3 | 0 | 0 | 0 | 0 | 2 | 2 |
| 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 3 | 0 | 0 | 0 | 4 | 4 | 0 |
| 0 | 0 | 0 | 0 | 0 | 4 | 4 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
이렇게 범위를 벗어나거나 새로운 땅에 닿을 떄까지 상하좌우로 직진한다.
모든 다리의 길이를 우선순위 큐에 넣었으니 이제 kruskal 알고리즘으로 MST만 만들면 된다.
소스코드
#include <iostream>
#include <vector>
#include <utility>
#include <queue>
using namespace std;
typedef pair<int, int> pp;
int N, M;
vector<vector<int>> board;
vector<int> parent;
priority_queue<pair<int, pp>, vector<pair<int, pp>>, greater<pair<int, pp>>> pq; //min-heap
pp dir[4] = {{-1, 0},
{1, 0},
{0, -1},
{0, 1}};
void dfs(pp cur, int mark) { //같은 구역의 섬을 같은 mark로 표시
board[cur.first][cur.second] = mark;
for (int i = 0; i < 4; i++) {
int nr = cur.first + dir[i].first;
int nc = cur.second + dir[i].second;
if ((nr >= 0) && (nr < N) && (nc >= 0) && (nc < M) && (board[nr][nc] == 1))
dfs(make_pair(nr, nc), mark);
}
}
void findBridge(pp cur) {
int row = cur.first;
int col = cur.second;
int mark = board[row][col];
for (int i = 0; i < 4; i++) { //상하좌우로 계속 다리 만들어보기
int tmp_r = row + dir[i].first;
int tmp_c = col + dir[i].second;
int dist = 0; //다리의 길이
while ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M) && (board[tmp_r][tmp_c] == 0)) { //범위 내에 있고, 바다인 동안 직진
tmp_r += dir[i].first;
tmp_c += dir[i].second;
dist++;
}
if ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M)) { //범위 내에 있고
if ((board[tmp_r][tmp_c] != mark) && (dist > 1)) { //새로운 섬인데 거리가 1보다 크다면 우선순위 큐에 넣기
pq.push(make_pair(dist, make_pair(mark, board[tmp_r][tmp_c])));
}
}
}
}
int findParent(int x) { //parent[x]가 음수가 될 때까지(root에 다다를 때까지) 재귀 함수 호출
if (parent[x] < 0)
return x;
return parent[x] = findParent(parent[x]);
}
bool unionInput(int x, int y) {
int x_p = findParent(x); //x의 부모
int y_p = findParent(y); //y의 부모
if (x_p == y_p) //이미 같은 집합, 이 간선 쓸 수 없음
return false;
if (parent[x_p] < parent[y_p]) { //x_p를 root로 하는 노드가 더 많으면 x_p -> y_p
parent[x_p] += parent[y_p];
parent[y_p] = x_p;
} else { //y_p를 root로 하는 노드가 더 많으면 y_p -> x_p
parent[y_p] += parent[x_p];
parent[x_p] = y_p;
}
return true;
}
int kruskalMst(int V) {
int cnt = 0, weight = 0;
while (!pq.empty()) {
if (cnt == (V - 1)) //다리의 수가 (섬의 수)-1 이라면 리턴
return weight;
int dist = pq.top().first;
int x = pq.top().second.first;
int y = pq.top().second.second;
pq.pop();
if (unionInput(x, y)) { //x, y를 유니온할 수 있다면
cnt++;
weight += dist;
}
}
return -1; //mst를 만들지 못함
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cin >> N >> M;
board.assign(N, vector<int>(M, 0));
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++)
cin >> board[i][j];
}
int idx = 2; //섬의 수 저장
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (board[i][j] == 1) //dfs로 각 섬마다 번호 매기기
dfs(make_pair(i, j), idx++);
}
}
parent.assign(idx, -1); //parent 벡터 할당
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (board[i][j] > 0) //해당 땅에서 만들 수 있는 다리 찾기
findBridge(make_pair(i, j));
}
}
cout << kruskalMst(idx - 2); //섬의 수는 (idx-2)개
}전체 소스코드다.
int idx = 2; //섬의 수 저장
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (board[i][j] == 1) //dfs로 각 섬마다 번호 매기기
dfs(make_pair(i, j), idx++);
}
}idx에 섬의 수가 저장될 것이다. 엄밀히 말하면 2부터 시작하니까 (섬의 수)+2가 idx가 될 텐데
아무튼 각 섬에 대해 dfs를 호출하며 각기 다른 mark로 표시한다.
void dfs(pp cur, int mark) { //같은 구역의 섬을 같은 mark로 표시
board[cur.first][cur.second] = mark;
for (int i = 0; i < 4; i++) {
int nr = cur.first + dir[i].first;
int nc = cur.second + dir[i].second;
if ((nr >= 0) && (nr < N) && (nc >= 0) && (nc < M) && (board[nr][nc] == 1))
dfs(make_pair(nr, nc), mark);
}
}그냥 평범한 dfs다.
parent.assign(idx, -1); //parent 벡터 할당그리고 섬이 총 몇 개인지 알았으니 사용한 idx만큼 parent 벡터를 할당하고 초기화 한다.
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (board[i][j] > 0) //해당 땅에서 만들 수 있는 다리 찾기
findBridge(make_pair(i, j));
}
}존재하는 모든 땅에 대해 findBridge 함수를 호출해 우선순위 큐를 채워준다.
물론 중복되는 값이 여럿 들어갈 수 있지만 범위가 작기도 하고 MST를 만들면서 걸러질 것이라 괜찮다.
void findBridge(pp cur) {
int row = cur.first;
int col = cur.second;
int mark = board[row][col];
for (int i = 0; i < 4; i++) { //상하좌우로 계속 다리 만들어보기
int tmp_r = row + dir[i].first;
int tmp_c = col + dir[i].second;
int dist = 0; //다리의 길이
while ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M) && (board[tmp_r][tmp_c] == 0)) { //범위 내에 있고, 바다인 동안 직진
tmp_r += dir[i].first;
tmp_c += dir[i].second;
dist++;
}
if ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M)) { //범위 내에 있고
if ((board[tmp_r][tmp_c] != mark) && (dist > 1)) { //새로운 섬인데 거리가 1보다 크다면 우선순위 큐에 넣기
pq.push(make_pair(dist, make_pair(mark, board[tmp_r][tmp_c])));
}
}
}
}findBridge 함수다.
int row = cur.first;
int col = cur.second;
int mark = board[row][col];먼저 시작지점의 행, 열 그리고 섬 라벨을 저장한다.
for (int i = 0; i < 4; i++) { //상하좌우로 계속 다리 만들어보기
int tmp_r = row + dir[i].first;
int tmp_c = col + dir[i].second;
int dist = 0; //다리의 길이
while ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M) && (board[tmp_r][tmp_c] == 0)) { //범위 내에 있고, 바다인 동안 직진
tmp_r += dir[i].first;
tmp_c += dir[i].second;
dist++;
}
if ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M)) { //범위 내에 있고
if ((board[tmp_r][tmp_c] != mark) && (dist > 1)) { //새로운 섬인데 거리가 1보다 크다면 우선순위 큐에 넣기
pq.push(make_pair(dist, make_pair(mark, board[tmp_r][tmp_c])));
}
}
}그리고 상하좌우로 뻗어나가며 다리를 만들어본다.
while ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M) && (board[tmp_r][tmp_c] == 0)) { //범위 내에 있고, 바다인 동안 직진
tmp_r += dir[i].first;
tmp_c += dir[i].second;
dist++;
}범위를 벗어나거나 땅에 닿을 때까지 직진한다.
if ((tmp_r >= 0) && (tmp_r < N) && (tmp_c >= 0) && (tmp_c < M)) { //범위 내에 있고
if ((board[tmp_r][tmp_c] != mark) && (dist > 1)) { //새로운 섬인데 거리가 1보다 크다면 우선순위 큐에 넣기
pq.push(make_pair(dist, make_pair(mark, board[tmp_r][tmp_c])));
}
}while문을 빠져나왔는데 여전히 범위 내에 있다면 땅에 도착했단 것이다.
그리고 그 땅이 mark가 아닌 다른 숫자라면 다른 섬에 닿은 것이다.
만약 이럴 때 dist도 1보다 크다면 유효한 다리이므로 우선순위 큐에 넣어준다.
cout << kruskalMst(idx - 2); //섬의 수는 (idx-2)개우선순위 큐를 다 채웠으니 이제 kruskalMst 함수로 MST를 만들면 된다.
int kruskalMst(int V) {
int cnt = 0, weight = 0;
while (!pq.empty()) {
if (cnt == (V - 1)) //다리의 수가 (섬의 수)-1 이라면 리턴
return weight;
int dist = pq.top().first;
int x = pq.top().second.first;
int y = pq.top().second.second;
pq.pop();
if (unionInput(x, y)) { //x, y를 유니온할 수 있다면
cnt++;
weight += dist;
}
}
return -1; //mst를 만들지 못함
}이 문제에선 MST를 못 만드는 경우가 있단 걸 고려해야 한다.
그래서 while문의 종료조건을 우선순위 큐가 비어있을 때로 하고, 중간중간 cnt==(V-1)이라면 리턴한다.
만약 리턴되지 않은 채로 while 문이 종료됐다면 MST를 만들지 못했다는 뜻이니 -1을 리턴한다.




