[백준] 2263번 : 트리의 순회

문제

 

---

풀이

 

inorder는 (왼쪽 트리)(루트)(오른쪽 트리) 순서로 탐색한다.

postorder는 (왼쪽 트리)(오른쪽 트리)(루트) 순서로 탐색한다.

 

1991번의

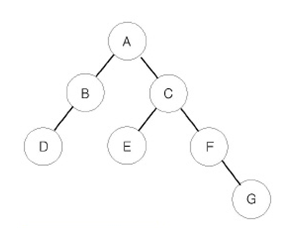
이 트리를 숫자로 바꿔보자.

 

inorder 순회는 4 2 1 5 3 6 7 이고

postorder 순회는 4 2 5 7 6 3 1 이다.

 

postorder 순회의 맨 마지막 값인 1(=A)가 트리의 최상위 root 노드인 것을 확인할 수 있다.

1을 기준으로 inorder를 나눠보면 (4 2)(1)(5 3 6 7)이 된다.

4(=D), 2(=B)는 A의 왼쪽 트리 요소이고, 5(=E), 3(=C), 6(=F), 7(=G)는 A의 오른쪽 트리 요소다.

 

루트노드를 기준으로 왼쪽, 오른쪽 트리로 분할해나가며 트리를 구하면 된다.

사실 preorder는 (루트)(왼쪽 트리)(오른쪽 트리) 순서로 탐색해서 트리를 만들 것 없이 그냥 바로 루트를 출력해도 괜찮지만, 난 트리를 직접 구현해보고 싶어서 그러지 않았다.

 

근데 계속 쪼개지는 배열 속에서 어떤게 postorder 기준 맨 오른쪽 데이터(root_data)인지 어떻게 알까?

root_data(=A, 1)를 기준으로 postorder를 나누면 4 2 | 5 7 6 3 | 1이 된다.

 

일단 오른쪽 트리의 새로운 root_data는 3이 된다. 그리고 이건 기존의 root_data인 1의 바로 왼쪽에 위치한다.

이전의 루트 인덱스를 pos라고 하면 오른쪽 트리의 루트 인덱스는 pos-1이 된다.

 

왼쪽 트리의 새로운 root_data는 2다. 그리고 이건 기존의 root_data인 1에서 root의 오른쪽 트리 요소 개수인 4에 1을 더한 만큼 건너뛴 왼쪽에 위치한다. 그럼 왼쪽 트리의 루트 인덱스는 pos-1-(root의 오른쪽 트리 요소 개수)가 된다.

root의 오른쪽 트리 요소 개수는 어떻게 구할까?

이건 inorder의 right 값인 6에서 root의 인덱스인 2를 뺀 4다. 정리하면 (pos-1)-(right-root_idx)인 것이다.

---

소스코드

 

#include <iostream>
#include <vector>
#include <map>
#include <utility>
#include <algorithm>

using namespace std;

vector<int> in, post;
map<int, pair<int, int>> tree;

int makeTree(int left, int right, int root_pos) { //left, right -> inorder 범위, root_pos -> postorder 끝 값
    if (left > right) //분할 종료 조건
        return -1;
    int root = find(in.begin(), in.end(), post[root_pos]) - in.begin(); //루트노드의 idx
    int left_node = makeTree(left, root - 1, (root_pos - 1) - (right - root)); //right-root = root의 오른쪽 자식들의 수
    int right_node = makeTree(root + 1, right, root_pos - 1); //root의 오른쪽 자식 값은 root_pos 바로 왼쪽에 위치
    tree[in[root]] = make_pair(left_node, right_node); //트리 생성
    return in[root]; //root 반환
}

void preorder(int node) { //preorder 출력
    cout << node << ' ';
    if (tree[node].first != -1)
        preorder(tree[node].first);
    if (tree[node].second != -1)
        preorder(tree[node].second);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(NULL);

    int n, input;

    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> input;
        in.push_back(input);
    }
    for (int i = 0; i < n; i++) {
        cin >> input;
        post.push_back(input);
    }
    int root_node = makeTree(0, in.size() - 1, in.size()-1);
    preorder(root_node);
}

전체 소스코드다.

 

map<int, pair<int, int>> tree;

트리는 map, pair 라이브러리로 구현한다.

map[1].first는 정점 1의 왼쪽 트리이고, map[1].second는 정점 1의 오른쪽 트리다.

 

    int root_node = makeTree(0, in.size() - 1, in.size() - 1);
    preorder(root_node);

makeTree 함수를 실행하고 난 뒤, root_node에는 최상위 정점이 저장된다.

그 이후 preorder 함수로 순회할거다.

 

int makeTree(int left, int right, int root_pos) { //left, right -> inorder 범위, root_pos -> postorder 끝 값
    if (left > right) //분할 종료 조건
        return -1;
    int root = find(in.begin(), in.end(), post[root_pos]) - in.begin(); //루트노드의 idx
    int left_node = makeTree(left, root - 1, (root_pos - 1) - (right - root)); //right-root = root의 오른쪽 자식들의 수
    int right_node = makeTree(root + 1, right, root_pos - 1); //root의 오른쪽 자식 값은 root_pos 바로 왼쪽에 위치
    tree[in[root]] = make_pair(left_node, right_node); //트리 생성
    return in[root]; //root 반환
}

makeTree 함수다.

find 함수를 이용해 inorder에서의 root의 인덱스를 구한다.

그리고 이 root를 기준으로 왼쪽 오른쪽으로 나눠 재귀호출을 한다. 그 결과들은 각각 left_node, right_node에 저장한다.

 

in[root]에 root 정점의 값이 존재한다. 재귀가 끝나면 얘에 대한 트리를 만들고 루트를 리턴한다.

 

void preorder(int node) { //preorder 출력
    cout << node << ' ';
    if (tree[node].first != -1)
        preorder(tree[node].first);
    if (tree[node].second != -1)
        preorder(tree[node].second);
}

간단한 prorder 순회 함수다.